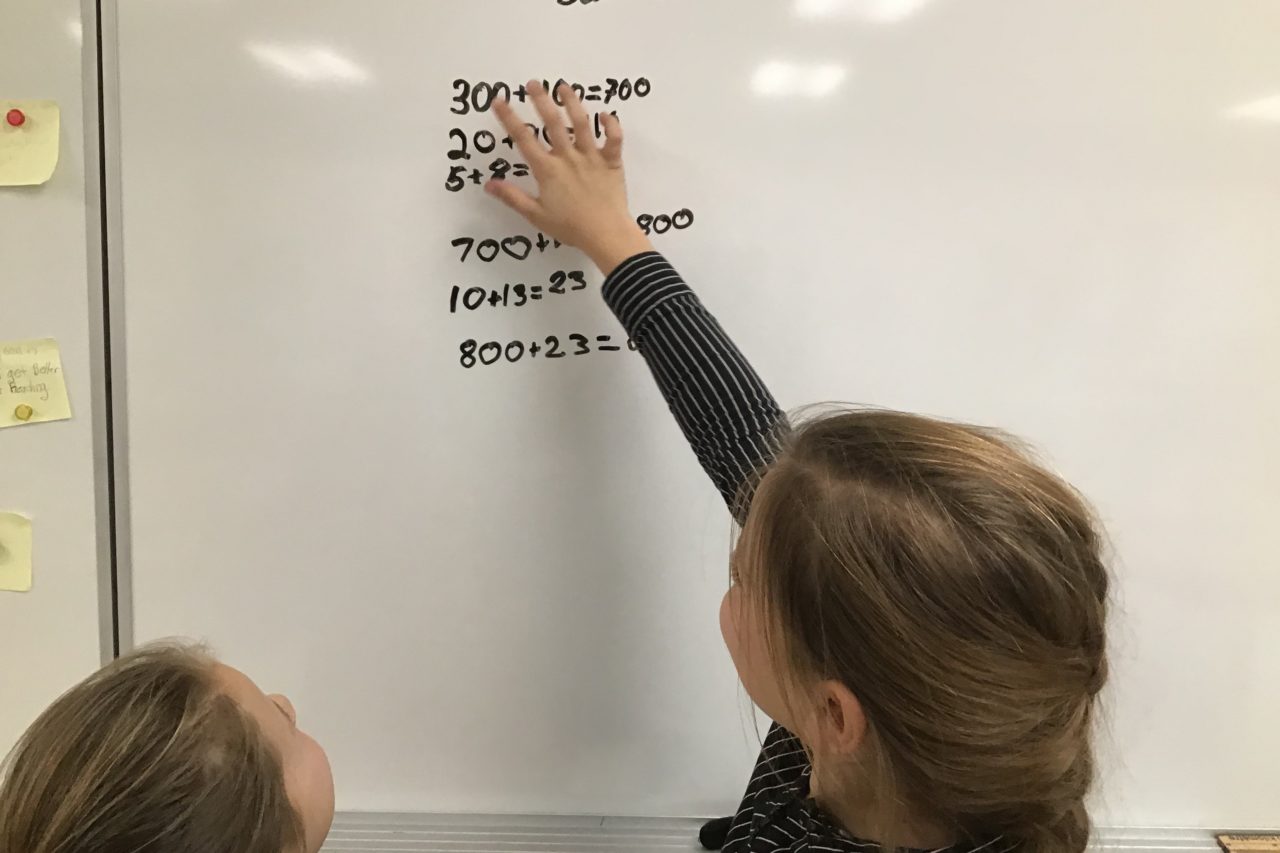What is Mathematical Competence?
As teachers, whether at PD sessions or in colleague conversations, most of us have had a conversation around what makes a student competent in math. A recent mRLC session in Portage La Prairie with Carole Fullerton began with this question, “What is mathematical competence?” After dialogue, we, as a group of teachers around the province, came up with the following:
- conceptual understanding
- fluency with the facts
- strategic competence (students have strategies to try in their toolbox)
- an ability to apply particular strategies depending on the scenario
- being metacognitive
- a productive disposition with an ability to persist and problem solve
To expand on this thinking around mathematical competence, Robert Barry, president of the National Council of Teachers of Mathematics (NCTM) recently wrote in a blog post expressing that,
“Promoting and valuing students’ participation in mathematical discourse–sharing their reasoning; creating, critiquing, and revising arguments; and engaging in collaborations aimed at making sense of and using mathematical ideas–is a way of positioning them as being mathematically competent.”
Teaching Through Problem Solving
So what context can we, as teachers, provide for our students to do this? One way is to use rich math problems. In the last number of years, divisional Professional Development, and consequently Hanover teachers, have focused on the works, words and wisdom of experts and researchers in the field such as John Van de Walle, Jo Boaler, Tracy Zager, Peter Lillejedahl, Carole Fullerton and John Hattie. As a result, many teachers have shifted from using a teaching-for-problem solving approach to teaching math through problem solving. More open-ended problems are now being posed with the intent to help students develop the concepts, competencies, and skills needed to grow as mathematicians. This might look like students working on rich, open-ended questions in small groups, often on vertical, non-permanent surfaces (whiteboards, windows, etc.) and practicing mathematical talk while using and sharing multiple, varied strategies. Time is given to students sharing mathematical thinking and reasoning of both individuals and across small groups. Teacher-facilitated sharing, reflection, and consolidation time brings the learning to a deeper level.
Importance of Good Questions
Good questions in a problem are important. Fullerton discussed some of them at her session:
- How many ways…? (invites multiple solutions and promotes fluency and flexibility)
- What might it be?
- How can you….? How do you know? (focus on exploring strategies for arriving at an answer)
- True or false? Would you rather…? (provides two options and both parts of the question require solving with a decision being made between alternatives)
- What do you know about…? (formative assessment)
- What can you find out about…? (invitation to inquire)
Student Talk
Student talk has great value and includes listening to others’ ideas, coming to see the varied approaches in how problems can be solved, making connections between ideas, reasoning, and practicing using proper mathematical terminology. We all know this doesn’t easily happen without scaffolding, and reinforcement through setting up positive norms in math class, incorporating warm-ups for building fact fluency, and mini lessons that develop conceptual understanding. These can be interwoven with
frequent problem solving tasks. The benefits of using open ended problems also include the intentional fostering of transferrable communication, critical thinking, and collaboration skills. John Hattie’s words found in his book, Visible Learning for Mathematics, Grades K-12: What Works Best to Optimize Student Learning reinforces this:
“Humans learn better when they interact with other humans. Students learn a lot more language when they are required to produce language. One of the best ways to do this is to have them collaborate with peers in solving complex, rich tasks.”
Hattie points out that, based on extensive research, the effect size for co-operative vs. individualistic learning is 0.59 and classroom discussion is 0.82 (the hinge point for entering the zone of desired effects is 0.40). He clarifies that discussion is not the questioning cycle of Teacher initiates, Student responds, Teacher evaluates, where students are simply recalling and reproducing.
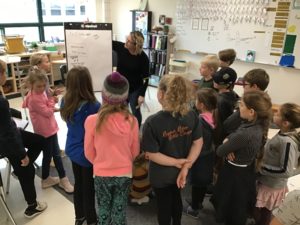
Classroom discussion and discourse allows students to speculate, hesitate, change their viewpoints, and take risks. Co-operative learning and classroom discussion are considered high impact strategies so all the more reason to have our students collaborating on problem solving and communicating their mathematical thinking together!
Teacher Reflections
Teachers Christine Friesen (Gr. 5) and Tawnya Klinkhammer (Gr. 3 / 4), both from Kleefeld School, were in attendance at Fullerton’s session and have been trying some of Fullerton’s Good Questions from her small flip books of open-ended math 
problems for Gr 2-4 and Grades 5-8. The inclusion of grouping random pairs of students, sharing of the whiteboard marker to foster collaborative thinking and mathematical talk, using vertical whiteboards and prompts like, “What did you do?” and “How else could you do it?” all supported students critically thinking and communicating together while building strategies for whole-number computation. Fullerton’s ‘good questions’ are strong building blocks to scaffold more complex problem solving.
Here are some of Tawnya and Christine’s recent reflections:
“I was able to quickly see the students’ understandings and misconceptions which made for authentic formative assessment. I was also able to easily see which students could use multiple strategies to manipulate numbers to arrive at a solution. These students also approached a problem in multiple ways. By communicating in small groups, I could see and hear students explaining their thinking verbally to peers and, by being able to explain it to others, I felt that a deeper understanding was being developed.” – Tawnya
“While my students were working on a Carole Fullerton question from her Good Questions book, I was able to note what the ‘go to’ strategies were that my students were most comfortable using. It was also interesting to hear their use of math vocabulary as they were verbalizing a variety of strategies with each other to show their thinking. Using Fullerton’s questions, having students sharing the pen, doing a gallery walk and then giving sharing and reflection time allowed this task to be more peer directed, as opposed to teacher directed.” – Christine
Check out the following links for some rich math tasks:
‘Open Middle’… challenging math problems worth solving
Numeracy Tasks – Peter Liljedahl
3 Act Math Tasks – Graham Fletcher
Others who create 3 Act Math Tasks: Andrew Gael Catherine Castillo Jon Orr
Kendra Lomax Kyle Pearce Mike Wiernicki Robert Kaplinsky Dane Ehler
nrich maths -primary curriculum mapping doc
Robert Kaplinsky – favourite lessons, why you use a problem, and a blog post to address five of the most common questions:
How long does it take to do a problem-based lesson?
How often do you do a problem-based lesson?
Do you use a problem-based lesson to begin a unit or after you’ve already taught them everything they need to know?
How is problem-based learning graded?
How long does it take to create a problem-based lesson?